OpenGL ES2入门03-理解图元类型
2019-08-30
概述
OpenGL中有三种图元类型,分别是点、线、三角形图元。我们在此着重理解一下线图元和三角形图元。
线
OpenGL ES支持以下几种类型的直线图元:
#define GL_LINES 0x0001
#define GL_LINE_LOOP 0x0002
#define GL_LINE_STRIP 0x0003

假设提供 n 个顶点,我们可以对直线图元类型做以下解释:
GL_LINES: 绘制一系列不相连的直线,共绘制 n/2条直线。GL_LINE_STRIP: 绘制一系列相连的直线,共绘制n-1条直线。GL_LINE_LOOP: 绘制一系列先练的封闭直线,共绘制n条直线。
示例程序
提供矩形的4个顶点
我们根据上述规则,画出三种图元下绘制的结果:
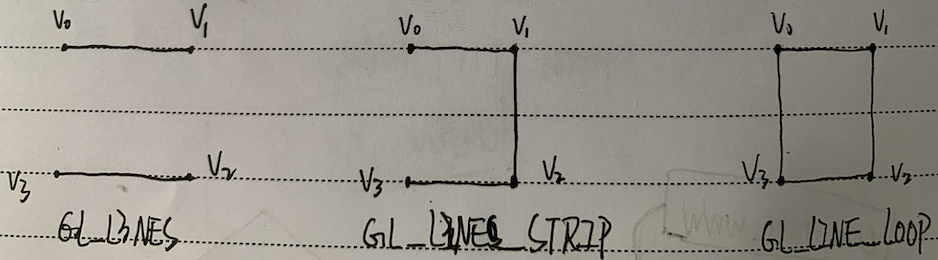
我们的示例程序OpenGL_02的结果如下:

提供八边形的八个顶点
我们根据上述规则,画出三种图元下绘制的结果:
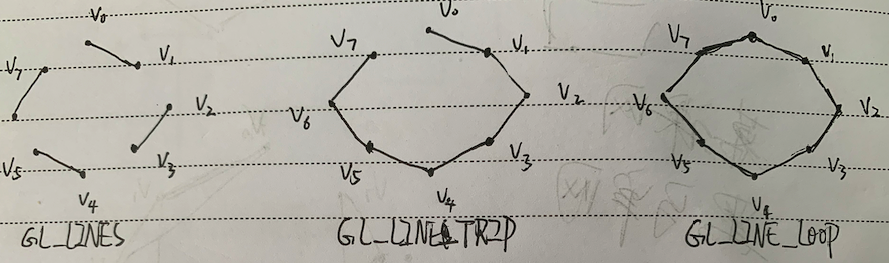
我们的示例程序OpenGL_02的结果如下:

三角形
OpenGL ES支持一下几种类型的三角形图元:
#define GL_TRIANGLES 0x0004
#define GL_TRIANGLE_STRIP 0x0005
#define GL_TRIANGLE_FAN 0x0006

假设提供 n 个顶点,我们可以对三角形图元类型做以下解释:
GL_TRIANGLES: 是以每三个顶点绘制一个三角形。第一个三角形使用顶点v0,v1,v2,第二个使用v3,v4,v5,以此类推。如果顶点的个数n不是3的倍数,那么最后的1个或者2个顶点会被忽略。共绘制 n/3个三角形。GL_TRIANGLE_STRIP: 这种类型的图元绘制规则略微复杂。其规律是: 构建当前三角形的顶点的连接顺序依赖于要和前面已经出现过的2个顶点组成三角形的当前顶点的序号的奇偶性(如果从0开始)。- 如果当前顶点是奇数:组成三角形的顶点排列顺序:T = [n-1 n-2 n].
- 如果当前顶点是偶数:组成三角形的顶点排列顺序:T = [n-2 n-1 n].
- 以上图为例,第一个三角形,顶点v2序号是2,是偶数,则顶点排列顺序是v0,v1,v2。第二个三角形,顶点v3序号是3,是奇数,则顶点排列顺序是v2,v1,v3,第三个三角形,顶点v4序号是4,是偶数,则顶点排列顺序是v2,v3,v4,以此类推。
GL_TRIANGLE_FAN: 绘制各三角形形成一个扇形序列,以v0为起始点,(v0,v1,v2)、(v0,v2,v3)、(v0,v3,v4)
示例程序
提供矩形的4个顶点
我们根据上述规则,画出三种图元下绘制的结果:
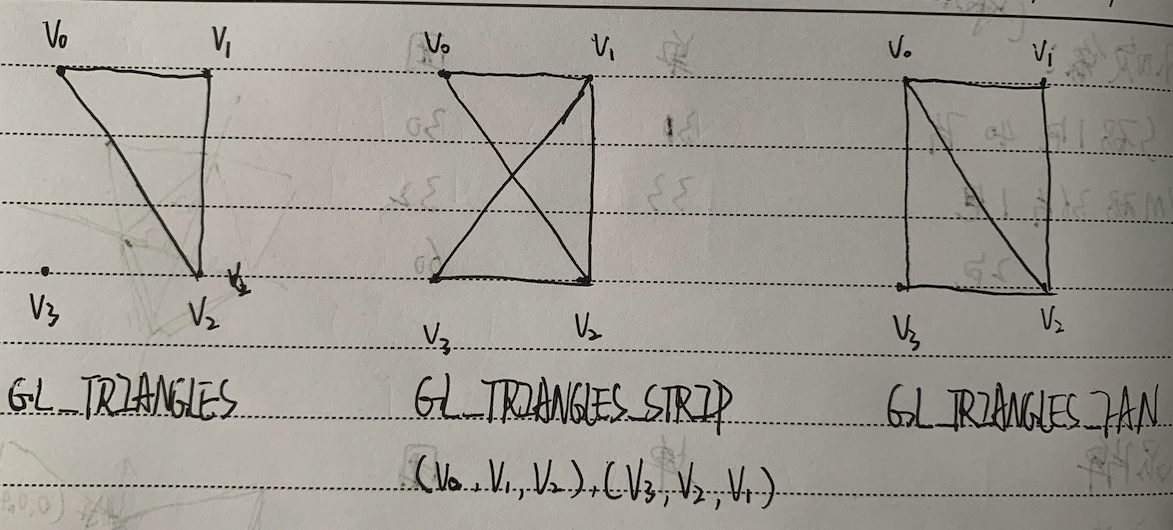
我们的示例程序OpenGL_02的结果如下:

提供八边形的八个顶点
我们根据上述规则,画出三种图元下绘制的结果:
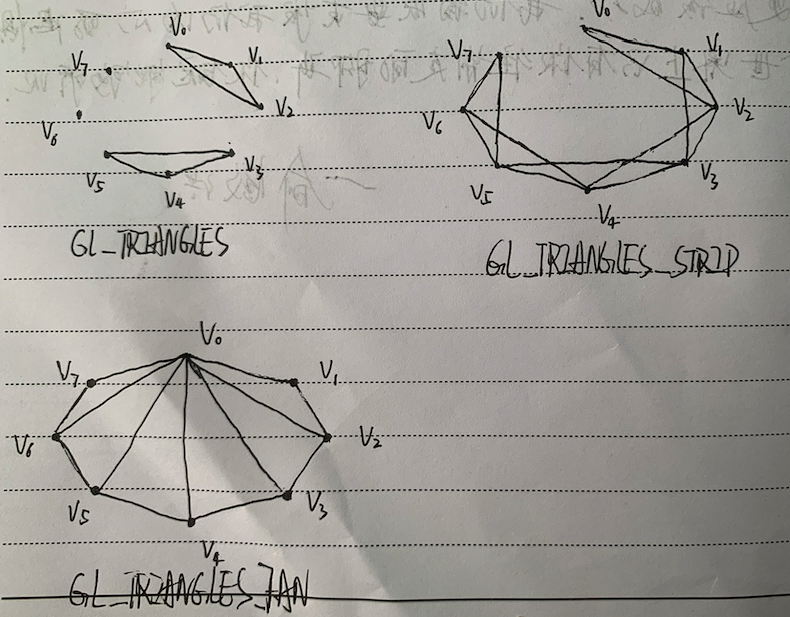
我们的示例程序OpenGL_02的结果如下:

