OpenGL ES2入门04-位移旋转缩放
2019-09-16
向量
在数学中,向量是指具有大小和方向的量。

如上图,向量v用公式表示为:
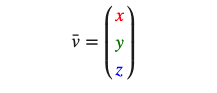
向量与标量运算
标量(Scalar)只是一个数字(或者说是仅有一个分量的向量)。当把一个向量加/减/乘/除一个标量,我们可以简单的把向量的每个分量分别进行该运算。对于加法来说会像这样:

其中的+可以是+,-,·或÷,其中·是乘号。注意-和÷运算时不能颠倒(标量-/÷向量),因为颠倒的运算是没有定义的。
向量取反
对一个向量取反(Negate)会将其方向逆转。一个指向东北的向量取反后就指向西南方向了。我们在一个向量的每个分量前加负号就可以实现取反了(或者说用-1数乘该向量):
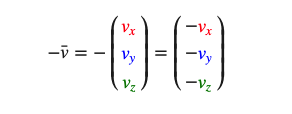
向量加减
向量的加法可以被定义为是分量的(Component-wise)相加,即将一个向量中的每一个分量加上另一个向量的对应分量:

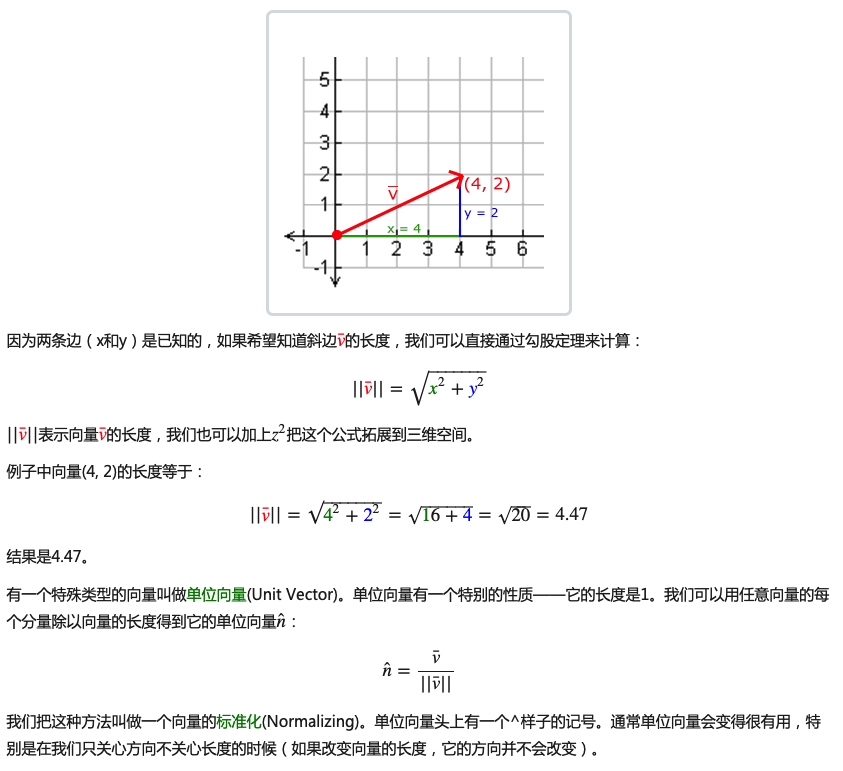
长度
我们使用勾股定理(Pythagoras Theorem)来获取向量的长度(Length)/大小(Magnitude)。如果你把向量的x与y分量画出来,该向量会和x与y分量为边形成一个三角形:
向量相乘
点乘
两个向量的点乘等于它们的数乘结果乘以两个向量之间夹角的余弦值。
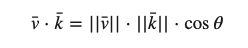
如果向量v和向量k都是单位向量,它们的长度会等于1。这样公式会有效简化成:
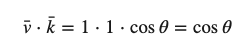
现在点积只定义了两个向量的夹角。你也许记得90度的余弦值是0,0度的余弦值是1。使用点乘可以很容易测试两个向量是否正交(Orthogonal)或平行(正交意味着两个向量互为直角)。
所以,我们该如何计算点乘呢?点乘是通过将对应分量逐个相乘,然后再把所得积相加来计算的。两个单位向量的(你可以验证它们的长度都为1)点乘会像是这样:
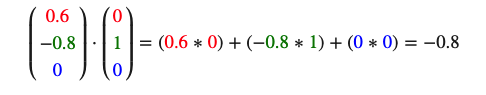
要计算两个单位向量间的夹角,我们可以使用反余弦函数 ,可得结果是143.1度。现在我们很快就计算出了这两个向量的夹角。点乘会在计算光照的时候非常有用。
叉乘
叉乘只在3D空间中有定义,它需要两个不平行向量作为输入,生成一个正交于两个输入向量的第三个向量。如果输入的两个向量也是正交的,那么叉乘之后将会产生3个互相正交的向量。接下来的教程中这会非常有用。下面的图片展示了3D空间中叉乘的样子:

不同于其他运算,如果你没有钻研过线性代数,可能会觉得叉乘很反直觉,所以只记住公式就没问题啦(记不住也没问题)。下面你会看到两个正交向量A和B叉积:

矩阵
由 m × n 个数aij排成的m行n列的数表称为m行n列的矩阵,简称m × n矩阵。记作:

这m×n 个数称为矩阵A的元素,简称为元,数aij位于矩阵A的第i行第j列,称为矩阵A的(i,j)元,以数 aij为(i,j)元的矩阵可记为(aij)或(aij)m × n,m×n矩阵A也记作Amn。
矩阵的加减
矩阵与标量之间的加减:

矩阵与矩阵之间的加减:
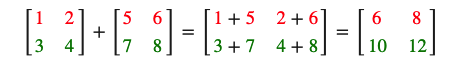
矩阵的数乘
和矩阵与标量的加减一样,矩阵与标量之间的乘法也是矩阵的每一个元素分别乘以该标量。下面的例子展示了乘法的过程:

矩阵相乘
矩阵乘法基本上意味着遵照规定好的法则进行相乘。当然,相乘还有一些限制:
- 只有当左侧矩阵的列数与右侧矩阵的行数相等,两个矩阵才能相乘。
- 矩阵相乘不遵守交换律(Commutative),也就是说A⋅B≠B⋅A。
我们先看一个两个2×2矩阵相乘的例子:

再看一个更复杂点的:

矩阵和向量相乘
我们用向量来表示位置,表示颜色,甚至是纹理坐标。让我们更深入了解一下向量,它其实就是一个N×1矩阵,N表示向量分量的个数(也叫N维(N-dimensional)向量)。如果你仔细思考一下就会明白。向量和矩阵一样都是一个数字序列,但它只有1列。那么,这个新的定义对我们有什么帮助呢?如果我们有一个M×N矩阵,我们可以用这个矩阵乘以我们的N×1向量,因为这个矩阵的列数等于向量的行数,所以它们就能相乘。
但是为什么我们会关心矩阵能否乘以一个向量?好吧,正巧,很多有趣的2D/3D变换都可以放在一个矩阵中,用这个矩阵乘以我们的向量将变换(Transform)这个向量。如果你仍然有些困惑,我们来看一些例子,你很快就能明白了。
单位矩阵
单位矩阵即是除了对角线以外都是0的NxN矩阵。在下示中可以看到,这种变换矩阵使一个向量完全不变:
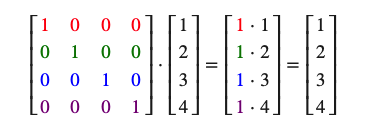
缩放
对一个向量进行缩放(Scaling)就是对向量的长度进行缩放,而保持它的方向不变。由于我们进行的是2维或3维操作,我们可以分别定义一个有2或3个缩放变量的向量,每个变量缩放一个轴(x、y或z)。
我们先来尝试缩放向量v¯=(3,2)。我们可以把向量沿着x轴缩放0.5,使它的宽度缩小为原来的二分之一;我们将沿着y轴把向量的高度缩放为原来的两倍。我们看看把向量缩放(0.5, 2)倍所获得的s¯是什么样的:
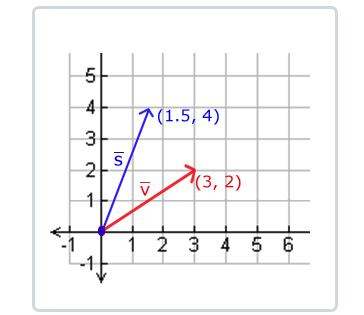
记住,OpenGL通常是在3D空间进行操作的,对于2D的情况我们可以把z轴缩放1倍,这样z轴的值就不变了。我们刚刚的缩放操作是不均匀(Non-uniform)缩放,因为每个轴的缩放因子(Scaling Factor)都不一样。如果每个轴的缩放因子都一样那么就叫均匀缩放(Uniform Scale)。
我们下面会构造一个变换矩阵来为我们提供缩放功能。我们从单位矩阵了解到,每个对角线元素会分别与向量的对应元素相乘。如果我们把1变为3会怎样?这样子的话,我们就把向量的每个元素乘以3了,这事实上就把向量缩放3倍。如果我们把缩放变量表示为(S1,S2,S3)我们可以为任意向量(x,y,z)定义一个缩放矩阵:
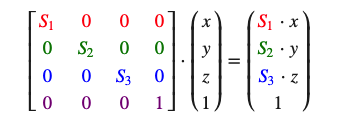
位移
位移(Translation)是在原始向量的基础上加上另一个向量从而获得一个在不同位置的新向量的过程,从而在位移向量基础上移动了原始向量。我们已经讨论了向量加法,所以这应该不会太陌生。
和缩放矩阵一样,在4×4矩阵上有几个特别的位置用来执行特定的操作,对于位移来说它们是第四列最上面的3个值。如果我们把位移向量表示为(Tx,Ty,Tz),我们就能把位移矩阵定义为:
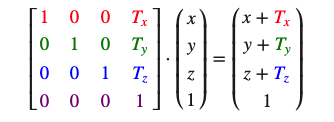
有了位移矩阵我们就可以在3个方向(x、y、z)上移动物体,它是我们的变换工具箱中非常有用的一个变换矩阵。
旋转
旋转矩阵在3D空间中每个单位轴都有不同定义,旋转角度用θ表示:
沿着x轴旋转:
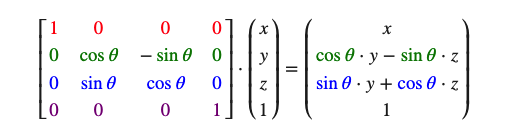
沿着y轴旋转:
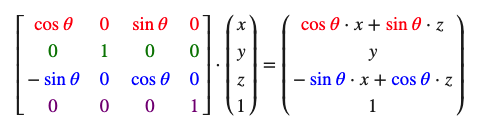
沿着z轴旋转:

对于3D空间中的旋转,一个更好的模型是沿着任意的一个轴,比如单位向量$(0.662, 0.2, 0.7222)$旋转,而不是对一系列旋转矩阵进行复合。这样的一个(超级麻烦的)矩阵是存在的,见下面这个公式,其中(Rx,Ry,Rz)代表任意旋转轴: